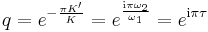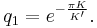Nome (mathematics)
In mathematics, specifically the theory of elliptic functions, the nome is a special function and is given by
where 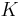 and
and 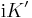 are the quarter periods, and
are the quarter periods, and  and
and 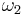 are the fundamental pair of periods. Notationally, the quarter periods
are the fundamental pair of periods. Notationally, the quarter periods 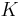 and
and 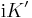 are usually used only in the context of the Jacobian elliptic functions, whereas the half-periods
are usually used only in the context of the Jacobian elliptic functions, whereas the half-periods  and
and 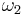 are usually used only in the context of Weierstrass elliptic functions. Some authors, notably Apostol, use
are usually used only in the context of Weierstrass elliptic functions. Some authors, notably Apostol, use  and
and 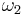 to denote whole periods rather than half-periods.
to denote whole periods rather than half-periods.
The nome is frequently used as a value with which elliptic functions and modular forms can be described; on the other hand, it can also be thought of as function, because the quarter periods are functions of the elliptic modulus. This ambiguity occurs because for real values of the elliptic modulus, the quarter periods and thus the nome are uniquely determined.
The function 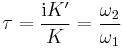 is sometimes called the half-period ratio because it is the ratio of the two half-periods
is sometimes called the half-period ratio because it is the ratio of the two half-periods  and
and 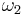 of an elliptic function.
of an elliptic function.
The complementary nome 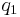 is given by
is given by
See the articles on quarter period and elliptic integrals for additional definitions and relations on the nome.
References
- Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. OCLC 1097832 . See sections 16.27.4 and 17.3.17. 1972 edition: ISBN 0486612724
- Tom M. Apostol, Modular Functions and Dirichlet Series in Number Theory, Second Edition (1990), Springer, New York ISBN 0-387-97127-0